
Altın Oran Tarihi
Altın oran, estetik denge ve uyum arayışında matematik ve sanatta önemli bir yer tutar. Antik dönemlerden günümüze kadar çeşitli sanat eserleri ve doğada kendine yer bulan bu oran, insan yaratıcılarının ilham kaynağı olmuştur. Matematiksel formülü ve doğal örnekleriyle derin araştırmalara açıktır.
Altın Oran Tarihi Altın oran, matematik ve sanat alanında önemli bir kavramdır. Bu oran, estetik bir denge ve uyum sağlamak amacıyla, birçok sanat eserinde, mimaride ve doğada kendine yer bulmuştur. Altın oranın tarihi, antik dönemlerden günümüze kadar uzanan bir yolculuğu kapsamaktadır. Antik Dönem ve Altın Oran Antik Yunan döneminde, matematikçiler ve sanatçılar, altın oranın estetik değerini keşfetmeye başladılar. Bu dönemde, Phidias gibi sanatçılar, Parthenon gibi eserlerinde altın oranı kullanarak, simetri ve dengeyi sağlamışlardır. Altın oran, "phi" (φ) sembolü ile gösterilir ve yaklaşık olarak 1.6180339887... değerine sahiptir.
Orta Çağ ve Rönesans Dönemi Orta Çağ'da, altın oran, sanatçılar ve mimarlar tarafından daha az dikkate alınsa da, Rönesans döneminde yeniden popülerlik kazanmıştır. Leonardo da Vinci, altın oranı eserlerinde sıkça kullanmış, "Vitruvian Adam" gibi çalışmalarında insan figürlerinin oranlarını altın oran ile ilişkilendirmiştir.
Modern Dönemde Altın Oran 20. yüzyılda, altın oran, sanat, mimari ve tasarım alanında önemli bir referans noktası olmaya devam etmiştir. Modern sanatçılar, bu oranı eserlerinde kullanarak, izleyicilere estetik bir deneyim sunmayı hedeflemişlerdir.
Altın Oranın Doğada Bulunması Altın oran, yalnızca sanat ve mimaride değil, doğada da sıklıkla karşımıza çıkmaktadır. Bitkilerde, hayvanlarda ve doğal oluşumlarda altın orana rastlamak mümkündür.
Sonuç Altın oran, tarih boyunca birçok kültürde, sanatta ve doğada önemli bir yer tutmuştur. Estetik, denge ve uyum arayışında bu oran, insanlığın yaratıcılık serüvenine katkıda bulunmuş, sanatçıların ve bilim insanlarının ilham kaynağı olmuştur. Günümüzde de altın oran, tasarım ve sanat alanında etkisini sürdürmekte, yeni nesil sanatçılar tarafından keşfedilmeye devam edilmektedir. Ekstra Bilgiler Altın oranın matematiksel formülü ve uygulamaları üzerine yapılan çalışmalar, bu konunun derinleşmesine ve daha fazla araştırma yapılmasına olanak sağlamaktadır. Ayrıca, altın oran, psikolojik ve bilişsel boyutta da incelenmektedir; çünkü insanlar genellikle bu orana sahip olan görüntüleri daha çekici bulmaktadır.
|
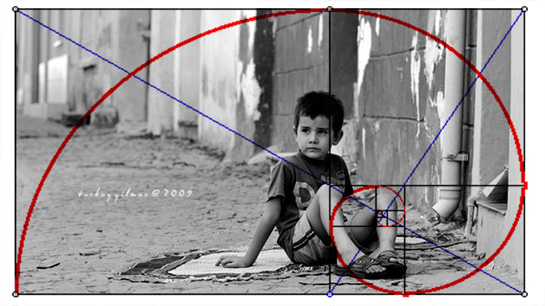

















Merhaba ben hep matematik e meraklıyımdır geçen yıl da üniversitemize matematik alanında bir uzman geldi ve matematik vee fizik hakkında birçok buluşştan bahsetti bunların arasında en dikkatimi çeken şey altın oran oldu altın oran nedir nasıl anlarız insanlarda ve ya herhangi bir eşyada mevcutmudur görür görmez ölçüm yapmadan anlamak mümkünmüdür
Merhaba! Altın oran, matematikte yaklaşık olarak 1.618'e eşit olan ve iki sayı arasındaki oranın, daha büyük olan sayının daha küçük olana oranına eşit olduğu bir orandır. Doğada, sanatta ve mimaride sıkça karşımıza çıkar. İnsanlarda ve nesnelerde altın oranı görmek için, bu oranı belirli ölçümler yaparak tespit etmek gerekir. Görür görmez anlamak zor olabilir, ancak gözün estetik algısı nedeniyle bazı durumlarda altın oranı içeren nesneler daha hoş ve dengeli gözükebilir.