
Altın Oran Nedir ve Nerede Kullanılır?
Altın oran, matematik ve sanatın kesişim noktasında yer alan estetik bir dengeyi temsil eden bir kavramdır. Phi (Φ) sembolü ile ifade edilen bu oran, doğada ve insan yapımı eserlerde sıkça gözlemlenir. Altın oran, hem matematiksel hem de estetik açıdan önemli bir unsurdur.
Altın Oran Nedir?Altın oran, matematik ve sanat alanlarında sıkça karşılaşılan ve estetik bir dengeyi temsil eden bir oran olarak tanımlanabilir. Genellikle "Phi" (Φ) sembolü ile gösterilen bu oran, yaklaşık 1.6180339887... sayısına karşılık gelir. Altın oran, iki miktarın birbirine oranı olarak ifade edilir; bu oran, daha büyük olan miktarın daha küçük olan miktara oranı ile, toplam miktarın daha büyük olan miktara oranı arasında bir eşitlik sağlar. Matematiksel olarak, bir 'a' ve 'b' sayısı için altın oran, aşağıdaki eşitlik ile tanımlanır:\[ \frac{a + b}{a} = \frac{a}{b} = \Phi \] Altın Oranın Tarihsel Gelişimi Altın oran, antik çağlardan bu yana sanatta ve mimaride estetik bir ilke olarak kullanılmıştır. Eski Yunanlılar, bu oranı mimari eserlerinde ve heykellerinde uygulamışlardır. Örneğin, Partenon Tapınağı'nın oranları altın orana dayanmaktadır. Ayrıca, Rönesans döneminde sanatçılar ve bilim insanları, altın oranı kompozisyonlarında ve eserlerinde kullanarak bu estetik anlayışı daha da yaygınlaştırmışlardır. Leonardo da Vinci'nin eserlerinde de altın oranın izleri görülmektedir. Altın Oranın Matematiksel Özellikleri Altın oranın matematiksel özellikleri, onu diğer oranlardan ayıran bazı önemli unsurlar içerir. Bu özelliklerden bazıları şunlardır:
Altın Oranın Sanat ve Tasarımda Kullanımı Altın oran, sanat ve tasarım alanlarında estetik bir denge sağlamak amacıyla kullanılmaktadır. Bu oran, birçok sanat eserinin kompozisyonunda, mimari yapıların tasarımında ve grafik tasarımda gözlemlenebilir. İşte altın oranın kullanıldığı bazı alanlar:
Altın Oranın Doğadaki Yansımaları Altın oran, doğada da sıkça rastlanan bir orandır. Bitkiler, hayvanlar ve doğal oluşumlar gibi birçok doğal yapıda altın oranın izleri görülebilir. Örneğin:
Sonuç Altın oran, matematiksel bir kavram olmanın ötesinde, estetik bir denge ve uyum sağlayan önemli bir ilkedir. Sanat, mimari, doğa ve tasarım gibi birçok alanda kendine yer bulan bu oran, insanların görsel algısını etkileyen ve estetik bir değer sunan bir unsurdur. Altın oran, tarih boyunca sanatçılar ve bilim insanları tarafından incelenmiş ve uygulanmış, günümüzde de hala önemini korumaktadır. Bu bağlamda, altın oranı anlamak ve kullanmak, estetik bir bakış açısı geliştirmek isteyenler için vazgeçilmez bir unsurdur. |
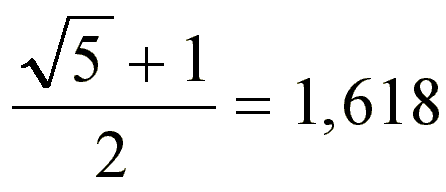

















Altın oran konusunu okuduktan sonra, gerçekten de doğanın ve sanatın ne kadar uyumlu bir matematiksel yapıya sahip olduğunu bir kez daha fark ettim. Bu oran, sadece mimaride değil, aynı zamanda doğadaki birçok canlıda ve cansız varlıkta da kendini gösteriyor. Örneğin, insan vücudunda altın oranın nasıl işlendiğini düşünmek oldukça ilginç. Kolların ve bacakların oranları, bu oranın doğada nasıl yer aldığını somut bir şekilde gösteriyor. Eldeki bilgiler ışığında, altın oranının tarih boyunca nasıl kullanıldığını ve günümüzdeki önemini anlamak da oldukça etkileyici. Mimarların ve tasarımcıların bu orandan faydalanarak eserlerine estetik bir değer katması, bu matematiksel oranı sadece bir sayı olmaktan çıkarıp, sanatsal bir ifade biçimi haline getiriyor. Sonuç olarak, altın oran sadece matematiksel bir kavram değil, aynı zamanda estetik ve doğanın bir yansıması olarak karşımıza çıkıyor. Bu oranı daha fazla öğrenmek ve hayatımda uygulamak için sabırsızlanıyorum.
Değerli Abdu'l-Melik,
Altın oran üzerine yaptığınız incelemeler gerçekten etkileyici. Bu matematiksel yapının doğada ve sanatta ne denli derin bir etki yarattığını fark etmeniz, konunun özünü anlamanızı gösteriyor. Altın oran, yalnızca estetik bir değer değil, aynı zamanda evrenin temel yapı taşlarından biri gibi görünüyor. İnsan vücudundaki oranlar ve simetri, doğanın bu matematiksel düzeninin bir yansıması olarak karşımıza çıkıyor.
Mimarların ve tasarımcıların bu oranı eserlerinde kullanmaları, estetik algıyı güçlendiriyor. Bu durum, sanatı ve bilimi bir araya getirerek, izleyicilere derin bir deneyim sunuyor. Altın oranı daha fazla öğrenme arzunuz ise, bu konuda ne kadar meraklı ve hevesli olduğunuzu gösteriyor. Bu tür matematiksel kavramların hayatımıza nasıl entegre edilebileceğini keşfetmek, kişisel gelişiminiz açısından da önemli bir adım olacaktır.
Umarım bu yolculuğunuzda ilham verici keşifler yaparsınız!
elerim koptu yazana kadar bukadarda olmaz ne zor sekizinci sınif,,,,,,,,,,,,,,,,,,,,
Bu sınavlar gerçekten çok yorucu olabiliyor ama emeklerinin karşılığını alacağına eminim. Az daha sabret!
Çok güzel bir sayfa ve çok fazla yazı var.Matemetik projem için teşekkürler&9786;
Rica ederim! Projenizde başarılar dilerim.